Romps, Latent heating is proportional to droplet radius and not droplet surface area, JAS, 2025
Paper
Description
A common misconception is that the rates of condensation, evaporation, and latent heating within clouds are proportional to the droplet surface area. In reality, given the relative humidity, cloud droplets condense or evaporate in proportion to their radius, not their surface area. This is an important distinction. Cloud A with 100 cm-3 of 16-μm droplets has twice the droplet surface area (per volume of air) as cloud B with 800 cm-3 of 4-μm droplets, but, given the same relative humidity, cloud A will evaporate or condense half as quickly as cloud B.
Here, the relationship between latent heating and the droplet radius is demonstrated by solving the partial differential equations governing the conduction of heat and diffusion of mass around an individual droplet. As expected, the heat rate is found to be proportional to the droplet's radius, not the droplet's surface area. Given a sudden perturbation (e.g., sudden onset of ascent, sudden onset of cooling, sudden change in supersaturation), the proportionality to the radius is established on a timescale of ~0.04—100 μs, which is safe to ignore when studying cloud dynamics.
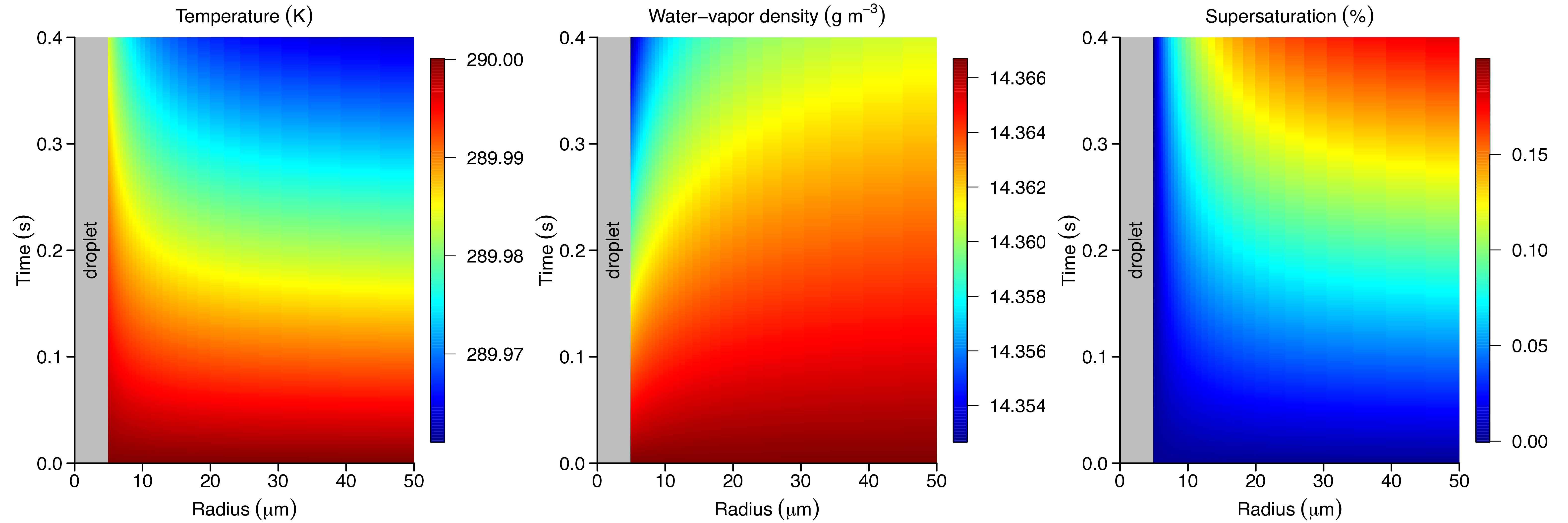
Zooming into the vicinity of a droplet in a cloud that is ascending at 10 m/s, the (left) temperature, (middle) water-vapor density, and (right) supersaturation within 50 microns of the droplet's center for the first 0.4 seconds of ascent. The cloud is initialized with a monodisperse distribution of droplets with a 5-micron radius, a liquid mass fraction of 10-5, a pressure of 90 kPa, a temperature of 290 K, and zero supersaturation.